对线性模型中的均值μ的理解
假设我们有一组数据,大致可能是这样的(随机生成,请勿当真):
| replicate | y |
|---|---|
| 1 | 102 |
| 2 | 98 |
| 3 | 100 |
| 1 | 98 |
| 2 | 101 |
| 3 | 101 |
| 1 | 101 |
| 2 | 100 |
| 3 | 101 |
| 1 | 101 |
| 2 | 98 |
| 3 | 101 |
在做分析的时候,我们一般会用到混合线性模型,该模型很可能是这样的:
y = μ + replicate + error
其中y是因变量,replicate是独立的自变量。另一种叫法是y是replicate的函数。我们最终需要根据replicate的值来预测y。这很好理解。
error是误差,服从正态分布,均值是0,标准差恒定。
在这个模型中,出现了一个均值μ,这个μ到底是做什么用的呢?
我们利用R来理解这个问题:
xxxxxxxxxx# 建立矩阵a <- c(rep(1:3,4),102,98,100,98,101,101,101,100,101,101,98,101)m <- matrix(a, 12)# 转换为数据框m <- as.data.frame(m)# 给数据的列命名colnames(m)<- c("rep", "y")# 输入模型model <- lm(y ~ rep, m)model
结果1:
Call: lm(formula = y ~ rep, data = m)
Coefficients:
(Intercept) rep2 rep3
100.50 -1.25 0.25
- Call里面显示的是我们输入的模型。
- Coefficients列出了截距以及其他因子距离截距的差。
我们看到,截距是100.5。在模型中,μ作为一个常数项,只可能影响截距,不会对斜率造成影响,那么这个截距是否就是均值μ呢?
我们计算一下均值:
xxxxxxxxxx# 计算y的均值mean(m$y)
结果2:
[1] 100.1667
很明显,截距并不等于均值μ,那么新的问题来了,这个截距100.5是怎么来的?
在结果1的Coefficients中,列名是这样的:(Intercept),rep2,rep3。那么我们就可以推测(Intercept)=rep1,即rep=1的均值。再次用R进行验证:
xxxxxxxxxx# 计算rep=1时,y的均值mean(m$y[which(m$rep==1)])# 顺便,计算rep=2时,y的均值(-1.25是相对值,在结果1中)mean(m$y[which(m$rep==1)]) - 1.25# rep=3时,y的均值(0.25是相对值,在结果1中)mean(m$y[which(m$rep==1)]) + 0.25
结果3:
[1] 100.5
[1] 99.25
[1] 100.75
结果刚好等于100.5,说明截距就是rep1。
如果对以上数据作图,我们可以获得一条回归线:
xxxxxxxxxx# 画散点图plot(m$rep, m$y)# 画回归线abline(model)
结果4(图1):
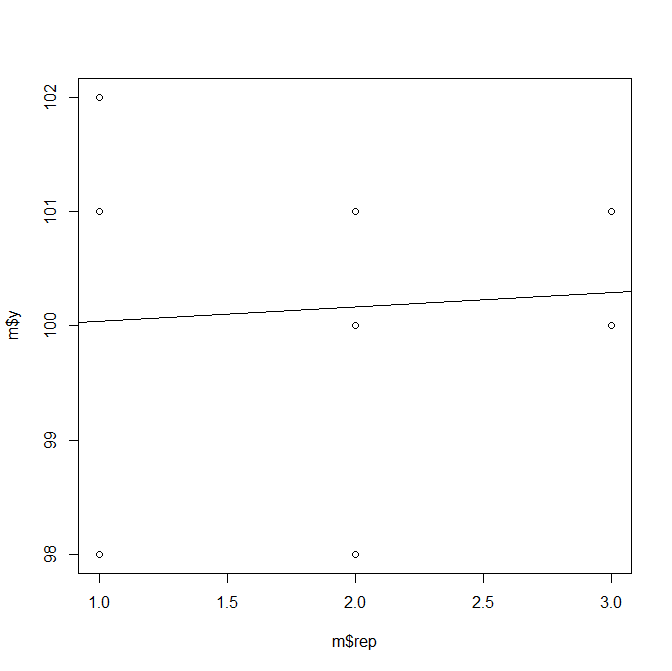
此图线如果还用原来的公式理解的话(y = μ + replicate + error),μ=0,ε=0,rep1=100.5,rep2=99.25,rep3=100.75。
我们将μ=100.2带入模型,则会得到μ=100.2,ε=0,rep1=100.5-100.2=0.3,rep2=99.25-100.2=-0.94,0.55。我们重新画图。
xxxxxxxxxx# y-μm2 <- mm2$y <- m2$y - 100.2# 输入模型model2 <- lm(y ~ rep, m2)# 画散点图plot(m2$rep, m2$y)# 画回归线abline(model2)
结果5(图2):
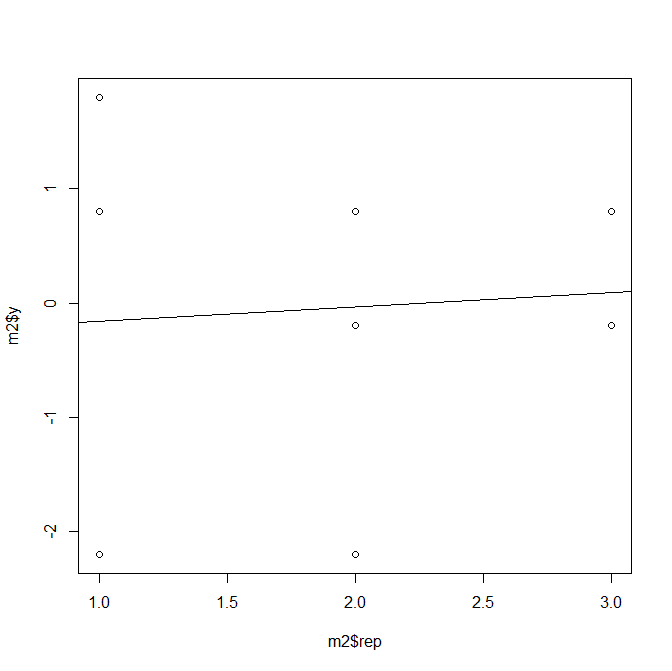
对比结果4和结果5,不难发现,除了纵坐标不同,两张图片是完全一样的。因此,μ的作用也就有了答案:
μ的实际作用就是设定一个截距,当然这个截距不一定非要由μ来承担:截距可以任意指定,比如说y中的任意值,例如,R中的截距选择的是y的第一个因子的均值;SAS中选择的是y中的最后一个因子的均值,这样做的目的是使曲线接近测定值。而使用均值μ,则是最简化的公式,即曲线最接近0,此时计算起来速度更快,数据量越大体现的越明显。
对模型来说,截距并不十分重要,重要的是斜率,改变截距不会对斜率造成任何影响。